数学と科学・技術 その4
みなさん、こんにちは。そして、今春から高校生になるみなさん、合格おめでとうございます。これからの高校生活を、ぜひ有意義なものにしてください。
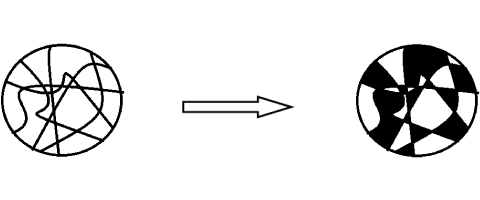
さて、今回はパズルのような話で始めることにします。下の図のように、円の中に、円周から円周に曲線を引いてみましょう。好きに引いてもらって構いません。
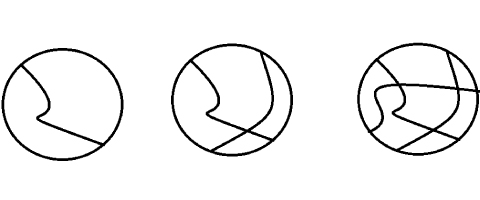
上の図では、曲線を1本、2本、3本の例を挙げました。すると、円の内側がいくつかの領域に分かれますが、この領域を、隣り合った領域は違う色になるように、白と黒で塗りつぶせるでしょうか?すこしやってみるとすぐ分かりますが、塗りつぶせることが分かります。下記のとおりです。
では、このような塗りつぶしはいつでもできるのでしょうか?実際にやってみた人は、出来そうだと感じるでしょうが、確かに多少複雑になっても、塗りつぶすことは可能です。
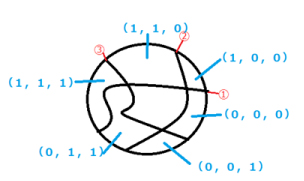
これはなぜでしょうか?やってみたらできるけど、ひょっとしたらできないものもあるでしょうか?実は、数学を使うと、できることがはっきり分かります。3つ曲線を引いた例で説明してみましょう。次の図のように、円の中に引いた曲線に①から③まで番号をつけます(赤字で番号をうっています)。そして、番号のついているところから、曲線に沿って進んでいったとき、右側が「1」、左側が「0」になるように番号をうってみましょう。
各領域が、水色で書いているように番号付けられます(真ん中の番号のついていない領域は、①の左、②の右、③の左なので「0, 1, 0」になります)。この番号を色分けに利用します。たとえば、こうして現れた数字をすべて足して、奇数になれば「黒」、偶数になれば「白」と約束して領域に色を塗ると、白黒の色分けができてしまうのです(真ん中の領域は 0+1+0=1 で奇数なので、黒色を塗ります。)。
いかかがでしょうか?「え、こんなことしてなんになるの?」と思われる人もいるでしょう。ところが実は、数学を使った色塗りは身近なところでも使われています。スーパーのレジでよく見るバーコードや、カメラ付き携帯電話で読み取るQRコードなどがその例です。
今回のパズルでは、白黒の塗りつぶしのために数学(2進法)を使いましたが、もっと複雑な数学のルールを使うことで、バーコードやQRコードのパターンが作られ、そこに情報を載せることで様々な利用がなされているのです。
数学というのは、きちんとルールを定め、客観的に問題を設定することで、さまざまな科学・技術の分野に応用されています。高校で習う数学は、出来るだけさまざまな分野に応用できるように、そして、分野の偏りが起きないように、基礎的な部分を教えられるため、時におもしろくないものと思えるかもしれません。ただ、そこで投げ出すと、その先にある風景を見ることができなくなってしまいます。
開成ハイスクール数学科 村上 豊