2016.02.22
このマジックには、「2進法という考え方をトリックに使っている」と、春香クリスティーンさんは言っていましたね。
では、2進法って何なのでしょう。これは、数学のある計算分野です。けっして難しい理屈ではないので、中学生はもちろん小学2年生のみんなも、理解できると思います。

さて、2進法を説明する前に、私たちが日常使っている、10進法についておさらいをしてみましょう。
10進法というのは、「0123456789」の10個の数字を使って、数をあらわす方法です。
ものを数えるときに、0からはじめて、8、9と進むと、その次の数をあらわすときには、9までしか数字が使えませんから、桁がひとつ繰り上がって、10の位を1として、1の位を0として、「10」とあらわす方法です。
これが、11、12・・・・・・・と進んで、98、99となった次は、100の位を1として、10の位、1の位をどちらも0として「100」とあらわしたのでしたね。まあ、10進法の考え方は、みなさんの常識でしょう。

2進法というのは「0」と「1」の2つの数字だけで、すべての数をあらわす方法です。
10進法の数を2進法ならばどのようにあらわすことができるか、見てみましょう。
| 十進法 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 二進法 | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 |

10進法の数を2進法であらわす方法は、1から順に書いていけば、なんとかできるようになったと思います。
でも、いきなり2進法で「10011」とあらわされた数を10進法であらわしなさい。などという問題が出たら、なかなか難しいですね。
この部分を理解するには、10進法の表記の理屈から見てみる必要があります。
例えば、10進法で23412という数は、2×104+3×103+4×102+1×101+2×100という理屈であらわされていることがわかるでしょうか。
103というように、10の右の上についた小さな数字は、「乗」と言いまして、103は、「10のさんじょう」とよみます。意味は、「10を3回かける」ということをあらわします。
ですから、
103=10×10×10=1000
ということになります。
ですから、
104=10×10×10×10=10000
102=10×10=100
101=10
そして100は、お約束として1となります。なんだか難しく感じた人もいるかもしれませんね。
でも、2×1万円札+3×千円札+4×100円玉+1×10円玉+2×1円玉=23412円と思えば、小学1年生でもわかる理屈ですね。
さて、先に示した2進法であらわされた10011ですが、1×24+0×23+0×22+1×21+1×20ということを意味します。10進法は、10の乗数ごとに桁が繰り上がっていきますが、2進法は、2の乗数ごとに桁が繰り上がっていくことになります。
だから、2進法であらわされた10011を10進法であらわすと、
1×24+0×23+0×22+1×21+1×20
=1×16+0×8+0×4+1×2+1×1
=16+2+1
=19
ということになるのですね。

10進法も2進法も、表し方は違いますが、ある数をひとつに決めることでは同じ役割を持っています。
例えば、10進法であらわされた1348という数を10進法で他の違う形であらわすことはできません。
同じ理屈で、2進法であらわされた1011(これは10進法では11になります)という数を2進法で他の違う形であらわすことはできません。
2進法がコンピューターなどの世界で使われている、と書きましたが、そのわけは2進法が使う数字が「0」と「1」の2種類しかないことです。コンピューターなどの世界では、スイッチのオンオフだけですべての数が表現できるので、広く用いられているのです。

ここが大切なところですが、2進法での各桁にでてきた、
「1」という数字は、その桁のあらわしている数が「ある」ことを意味していて、
「0」という数字は、その桁のあらわしている数が「ない」ことを意味していることに気がついてください。
先の2進法であらわされた10011が、
1×24+0×23+0×22+1×21+1×20
=1×16+0×8+0×4+1×2+1×1
=16+2+1
=19
だと、説明しましたが、各桁が意味している
24=16
23=8
22=4
21=2
20=1
という数が、「ある(=1)」「ない(=0)」かを10011という数字が意味していると理解してください。
この理屈は、ちょうど先の10進法で、1万円札や千円札を例にして説明したように、
1個ずつある、16g、8g、4g、2g、1gのおもりを使って、数をあらわしていると言い換えることができるかもしれませんね。
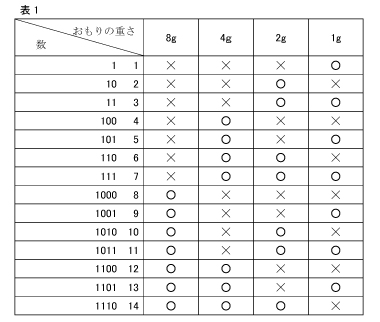
このように表にすると、1がそのおもりを使っていることをあらわし、0はそのおもりを使っていないことをあらわしていることに気がついたでしょう。

いよいよ、パジャマジックの種明かしです。
◇トリックその1
まず、春香クリスティーンさんが、示した4枚のシートには、いろいろな絵が描かれていましたが、それぞれの絵が、実は1から14までの特定の数字を意味する暗号でした。
あのシートの絵は、ただの絵ではなかったのですね。
| カードの絵 | いちご | ニンジン | さんま | しんぶん | ゴリラ | ろうそく | なみ |
|---|---|---|---|---|---|---|---|
| 数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| カードの絵 | ハブラシ | くり | とけい | はし | カレンダー | キング | たいよう |
|---|---|---|---|---|---|---|---|
| 数字 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
◇トリックその2
4枚のシートの左上に書かれた絵に注目!
左上に「いちご」の絵が描かれたシートには、1桁目が「1」になる2進法の数を意味していました。
同様に、「ニンジン」の絵が描かれたシートには2桁目が「1」になる数のことを、「しんぶん」の絵が描かれたシートには、3桁目が「1」になる数のことを、「ハブラシ」の絵が描かれたシートには、4桁目が「1」になる数のことを示していたのです。
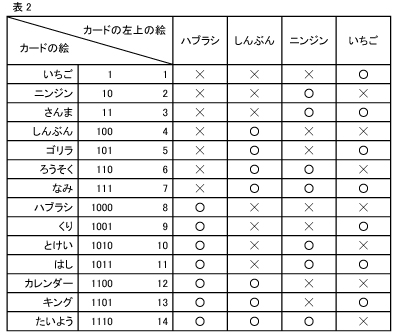
表2を見れば分かるように、ハブラシのシートには、4桁目が1になる数を意味する絵だけが描かれていました。ニンジンのシートには、2桁目が1になる数を意味する絵だけが描かれていたのです。 ◇そして種明かし マジックの相手の子どもたちは、「サンマ」の絵を選びました。サンマは3の意味で、21+1=3です。 サンマの絵は21つまり「2」を意味する「ニンジン」のシートと、1を意味する「いちご」のシートにだけ、「サンマ」は書かれています。 だから、マジックの相手が、左上の絵が「ニンジン」のシートと「いちご」のシートとに、「ある」と答えているので、その2つのシートが意味する2と1を足して、3、つまり、サンマを選んだことがわかるのです。 もしも、「ゴリラ」を選んだとしたら、ゴリラの5は、22+1=5ですから、 22つまり、「4」を意味する「しんぶん」のシートと、「1」を意味する「いちご」のシートだけに「ゴリラ」が書かれているので、マジックの相手が、しんぶんのシートとイチゴのシートに、「ある」と答えることになり、その2つのシートが意味する4と1を足して、5、つまり、ゴリラを選んだことがわかるのです。 では「はし」を選んだとすれば? そうですね、「はし」は11を意味していて、2進法では1011ですから、ハブラシとニンジンといちごのシートに、「ある」と相手が答えれば、8+2+1で11になるのですね。 これを読んでくれたみなさんは、2進法の理屈をきっと理解できたことでしょう。 春香クリスティーンの「パジャマジック」の解説編でした。

※掲載されている情報は、発表日現在のものです。その後、内容が変更になっている場合がありますので、あらかじめご了承ください。