新指導要領と数学(その3)
2013 年 2 月 18 日 月曜日 今回も前回(11月26日掲載分)に続いて、またまた新指導要領の話をしましょう。
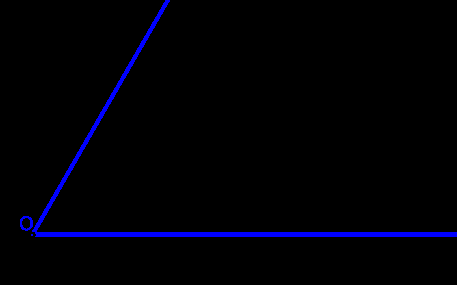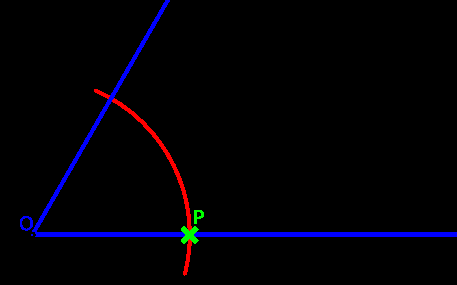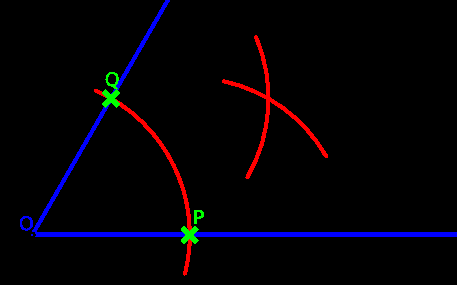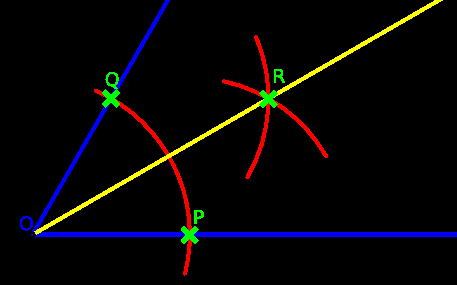
今回の指導要領の改訂で、「作図」が高校数学に入ってきました。まず、作図の問題とはどんな問題だったかを復習しましょう。「作図」とは、(目盛のついていない)定規とコンパスを使って色々な図形を描いていく問題でした。たとえば、与えられた角の二等分線の引き方は下の図のようになっています。
手順を言葉で書くと、(色で、図の中の手続きと、文章を対応させてますので、確認してください)
1)コンパスで円弧を描く
2)直線との交点を打つ
3)交点を中心に円弧を2つ描く
4)出来た交点を打つ
5)角の先端と交点を直線で結んで出来上がり
となります。
ところで、高校での作図(数学Aの範囲です)は、問題はもっと難しくなりますが、定規とコンパスのみという制限は何も変わりません。そこで、作図のことをあれこれ書くのではなく、定規とコンパスのみという制限を、数学の他の分野で習うこととの関連で書いてみます。
さて、作図における定規とは何をする道具でしょう。それは、直線を描く道具です。ところで直線は、中学の数学で、例えば、
![]()
という式で表すことができると習ったと思います。一方、コンパスは何をする道具でしょう。それは、円を描く道具です。円は高校の数Ⅱで、例えば、
![]()
と表すことができることを習います。だから何?と思う人もいるかもしれませんが、これで、定規とコンパスでできることを数式で表現できたのだ、ということを意識してみてください。数学はこのように現実の問題を数式で表現しているのだ、というように捉えることができます。でも、注意深く考えると、まだひとつだけ作図でできることで、数式で表現できてないことがあります。それは「交点を打つ」ということです。このことはどのように表現すればいいのでしょう。実はそれは、「上の2つの方程式を連立させて解く」、ということで表されているのです!では、「交点を打つ」ために連立方程式を解いてみましょう。直線の式を、円の式に代入してみると、
![]()
となって、なんと二次方程式を解くことになります!皆さんは何気なく交点を打っていたと思いますが、実は背後で二次方程式を解いていたのです。(後は方程式を解いて自分で交点を求めてくださいね。)
さて、作図の問題から始まり、二次方程式を解けばよい、ということまで話しました。数学は、実はこのようにいろいろな分野が絡み合っています。また、現実の問題とも密接にリンクしています。だからこそ、机上の勉強で終わらせるではなく、いろいろな経験と、学んでいることを結び付けることができるようになってください。もちろん、数学だけでなく、他の教科も忘れずに。
開成ハイスクール数学科 村上 豊



