新指導要領と数学(その7)
2013 年 12 月 30 日 月曜日みなさん、こんにちは。受験生のみなさんは、風邪などひいていないでしょうか?体調不良で全力を出せない、なんてことのないよう、普段の健康管理に気を付けてください。
さて、前回(10月15日)は、螺旋の話をしました。小学校からなじんできた図形(三角形や円)とは異なる図形でも、その周の長さを測ることが出来るのだ、ということをお伝えしました。では、三角形や円のような単純な図形を長い時間かけて学んできたのは何故でしょう?最初から、さまざまな図形を同等に扱って、知識をどんどん増やせばいいのではないでしょうか?
そこで、今回は三角形という単純な図形でも、意外とおもしろいことができるのだ、ということをお伝えして、三角形の復権をしたいと思います。なお、今回の話は新指導要領とは関係なく、旧課程から取り上げられてきた話題です。でも、あまり有名じゃないようなのでここで取り上げることにします。
さて、下の図形を見てください。
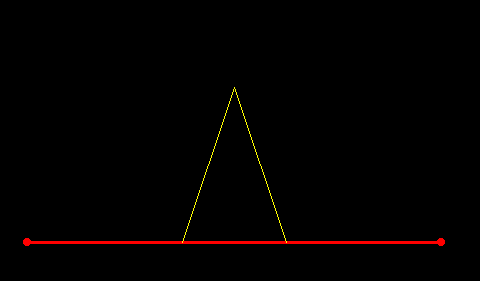
赤い線の上に黄色い三角形が乗っかっていますが、元の赤い線を三つに分けて、真ん中に黄色いでっぱりを作った、と考えてください。その結果、左端と右端の赤い線と2本の黄色い線で、計4つの線分が出来ています。そこで今度は、このできた4つの線分を、また三つに分けて、真ん中に黄色いでっぱりを作ります。すると次のような図形になります。
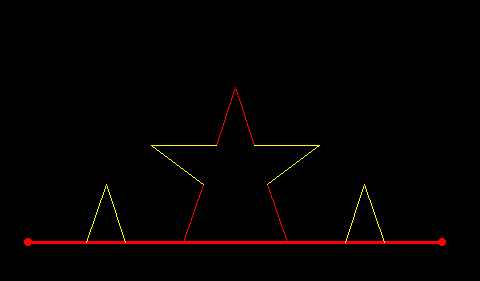
計16本の図形ができました。人によっては、真ん中に人間が立っているように見えるかもしれません。では、以下、このような操作を次々と繰り返していくとどうなるでしょう。
次のアニメーションを見てください。
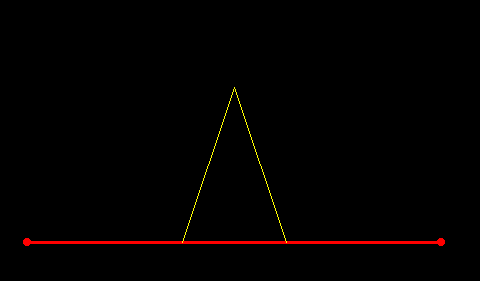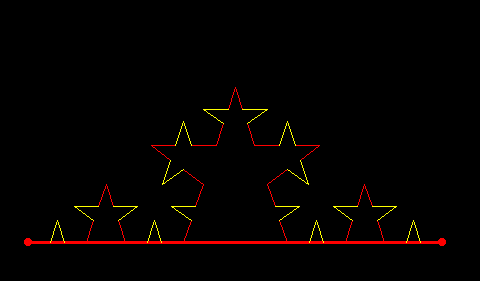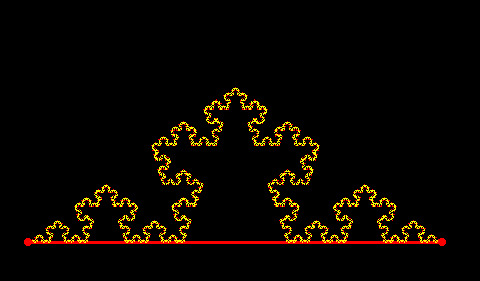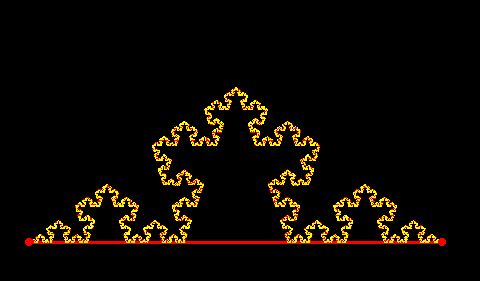
いかがでしょうか?きれいなイルミネーションができました。実は、この形を作るのに繰り返す操作を7回行って、線分の本数は4の8乗本=65536本になっています。繰り返す操作を増やせば、どんどん本数は多くなっていきます。無限に繰り返せば・・・本数は無限になって「コッホ曲線」と呼ばれるものになります。そしてこの曲線は、なんと、周の長さは無限!であるにも関わらず、囲まれている図形の面積は有限!!になっているのです。
いかがでしょうか?単純な三角形でもそれを組み合わせることで、意外と面白いものができるということが分かったでしょうか。数学は、単純なもの、単純な考え方を組み合わせて、いろいろなものを生み出したり、理解したりするのに役立ちます。学習指導要領という枠の中では見えてこないものも多いですが、学び続けることで多くのことを吸収してください。そして、特に受験生の方は、この冬に無事大学合格を勝ち取って、新たな扉を開けるように願っています。皆さんに幸いが訪れますように。
開成ハイスクール数学科 村上豊



