2017 年 9 月 18 日
2017年3月からスタートした今年度の授業も折り返しを過ぎました。私が管理する教室でも現役高校生達がこの半年間で大きな成長を見せてくれています。
高校1年生は、多忙な高校生活の中、塾における学習習慣も確立されてきました。また、授業の無い曜日にも自習室に通う生徒が増えました。勉強のスタミナも身に付き、数学の理解力や計算スピード・精度が向上しています。
高校2年生は、大学受験に対する意識が高くなってきました。自ら進んで大学の事を調べ、希望進路に関して思いを語ったり、授業前の隙間時間に自学習をする生徒も多くいます。一部理系の生徒を対象とした『数学Ⅲ特設講座』も開講され、高校よりも一足先に数学Ⅲの理解に努める生徒に対し、今後も熱い授業を展開していきます。
高校3年生は、夏を過ぎて目の色が変わってきました。公募制推薦入試の受験対策をする生徒、国公立大学志望でセンター試験の高得点を目指す生徒、国公立二次試験の記述力を磨き上げようとする生徒など、目標は人それぞれですが、良い緊張感の中で懸命に勉強しています。また、受験に向けて友情をさらに深め合おうとする姿を嬉しく思っています。
この半年間それぞれの『継続』があってこそ、今日の成長した姿があると確信しています。これから先、半年後の来春にさらなる成長と大きな成果をもたらしてくれることを期待し、皆の成長を見守っていきます。
開成ハイスクール数学科 中澤宏尚

カテゴリー: ブログ | コメントは受け付けていません。
2017 年 9 月 11 日
今年の4月、ある高校1年生の生徒が入塾してきました。
彼はサッカー部。日に焼けて真っ黒です。
部活はハードでしんどそうです。
しかし、ほぼ毎日自習室に来て勉強していました。
前期第一中間試験の結果は残念ながら良い成績ではありませんでした。
彼も悔しがっていました。私も悔しかったです。
努力しているのに…早く結果になってほしいと思っていました。
前期第二中間試験の結果は前回にくらべて大幅に成績アップ。
一緒になって喜びました。
そして夏期講習が始まりました。
夏期講習を受講しない生徒もいる中、彼は受講しました。
猛暑の中、彼は皆勤賞でした。
進研模試(全国模試)がありました。
先日、結果が返ってきました。
学年全体の総合成績順位は360人中16位。
一緒になって喜びました。
彼は1年生です。
しかし、1年生が一番差のつく学年。
彼には夢があります。
その夢を実現するために彼は毎日努力しています。
彼だけではありません。
高1の進研模試の数学で学年1位をとった生徒が鶴橋教室にいます。
彼はラグビー部です。
この夏、みんな精一杯やりきりました。
よく頑張ったと思います。
自習したり積極的に質問にきたりできる生徒が多かったのが印象的でした。
本当に感動した夏でした。ありがとう。
ハイスクール 英語科 大道英毅

カテゴリー: ブログ, 大学受験 | コメントは受け付けていません。
2017 年 9 月 4 日
一部の高校3年生は8月17日から新学期が始まっています。夏休み、本当に短くなってきましたね。新学期は9月から始まるというのは、もう昔話のようです。
毎年この時期になると、進路で悩む人が出てきます。あまり一人で抱え込まないようにしてくださいね。保護者・先生に色々疑問をぶつけてみてください。
高校1年生は、まずは文理選択がやってきます。将来就きたい職業、進みたい学部が決まっている人は問題ありませんが、まだまだそのような人は少ないです。大学入試に必要な科目を絞り込むいい機会なのですが、なかなか決められないのも現実です。私は英語と数学と理科が好きだったので、なんとなく理系を選択した記憶があります。これが後々大変なことになるんですが・・・。自分の適性を客観的に見つめるべき時期が来ているということです。他人のことは冷静に見えますが、いざ自分のこととなると見えないことも多くなるのが事実です。他人の意見に耳を傾けてみることもいいでしょう。もしここで間違った選択をしたとしても、遠回りにはなりますが、軌道修正のタイミングはありますので、自分の希望をいろんな人に聞いてもらって、それで判断してください。
高校2年生になると、ある程度現実が見えてきますので、本当に行きたいと思っている大学に関して、しっかりと調査をしてください。オープンキャンパスは秋以降にも実施されます。入学してから思っていたのと違うなんてことのないようにしてください。進路をより具体化すべきタイミングです。私はここで、自分の物理への適性のなさにようやく気付いて、文転することになりました。できればみなさんにはこのような回り道をしてもらいたくないので、やはり高校1年生の選択って今更ながら重要ですね。進路決定の最終リミットだと思ってください。
高校3年生は、指定校推薦にも悩まされます。本当に行きたい大学の行きたい学部の推薦が来ていれば迷わず取りに行くべきですが、大体がそうではないです。本当にその学部で、自分の夢がかなうのか、冷静に考えてください。先日もある女の子が私のところに相談にきました。同志社大学の○○学部の指定校推薦がきているのですが、どうしたらよいかということでした。その子の第一志望でないことはわかっていたので、逆にその学部に行ってその後どうするか考えましたかと質問すると、答えに困ってしまいました。これではいけません。本当に納得のいく選択をしてもらいたいので、再考していただきました。公募制推薦は、行きたい気持ちがあれば受験機会を増やすためにもどんどん出願すべきです。しかし、受験料も無料ではありません。このタイミングになっても保護者と話し合いをしていないのは論外です。身内に真面目な話をすることが恥ずかしいのは当然理解できます。しかし、それを避けることができない時期に来ているのです。
各学年とも新学期を迎えるにあたって、色々と悩みは出てくると思います。いろんな人の意見を聞いてください。そして、納得のいく判断をしてください。大事なことは、謙虚に自分を見つめるということです。難しいことですが、なんとか乗り越えてもらいたいと願っています。
開成ハイスクール 英語科 濱田健太郎


カテゴリー: 大学受験 | コメントは受け付けていません。
2017 年 8 月 28 日
みなさん、数学ってどういうイメージがありますか?
難しい問題を前に「うぅ~ん……」と時間をかけて悩んでいる姿を想像する人が多いのではないでしょうか。
ですが、それは違うんですよ!
受験数学において1番大切なのは難しい問題に時間をかけて悩むことではありません。基本的な問題の解法を理解して、応用問題で基本的な問題の解法の組み合わせ方を学ぶことが1番大切です。大学受験の数学の問題はどんなに難しい問題でも、基本的な問題の組み合わせですから。
では、解法を学んでいく段階で新しい問題を解くときの効率のよい勉強方法を紹介します。
1.問題を解く
とりあえず、解けるところまで解いてみましょう。ただし、考える時間は5分まで。
5分考えて分からない場合は解答を見ます。これが大切です。解法を知らないと全く進まないことが多いので、分からないのに考え続けることは時間の無駄になります。
2.答え合わせをする
「解答を見て納得して終わり」ではダメです!解けなかった問題を解けるようにすることが1番大切ですから、優先順位をつけて復習していく必要があります。そのための方法がマーク勉強法です。具体的には…
・解答を見ずに、しっかり解けた問題には〇
・解き方は分かっているが途中で計算ミスをした、詰まってしまった問題には△
・解き方の方針が全く分からない問題には×
を問題番号の横に書いていきます。
このとき、△や×の問題にはどこで詰まってしまったのかを解答にメモ書きしておくことが大切です。
後で解法を思い出すきっかけになることがあります。
3.復習する
効率良く点数を上げるために最も重要なことが、この復習になります。1回見ただけで確実に解法を身につけることができる人はそういませんからね。だだ、解けた問題を繰り返しても効果が薄いですから、優先順位をつけて復習していきましょう。
・〇の問題
何も見ずに1度解けた問題は、これから先も解けるので復習の必要はありません。ですが、それでは不安な人もいるでしょうから、復習したいという人は月に1度くらい見直しをしておきましょう。
・△の問題
計算ミスはなぜ計算ミスをしたのか確認をしてください。詰まった場合はその詰まったところが問題のポイントですから、きちんと理解して反復しましょう。アウトプットできるようになるまで徹底的に取り組むことが大切です。
・×の問題
手も足もでなかった問題ですから、まずは解法のポイントや問題の方針を何度も読んで確認し、△にしましょう
数学が苦手な人も得意な人もこの流れで取り組んでいけば、効率よく点数を上げていくことができます。
あとは……自分に厳しく「やりきる」だけです!!
開成ハイスクール数学科 中嶋 由博


カテゴリー: ブログ, 大学受験 | コメントは受け付けていません。
2017 年 8 月 21 日
夏休みの課題で、高校3年生の中には「生物」「基礎生物」を完成させる目標を持たれている方も多いでしょう。英数国と異なり、積み重ねの勉強は必要ではなく、ある程度短期に集中して勉強すれば得点源にできる科目です。まずどこからスタートすればよいか、どのように勉強すればよいかを「知識問題」「グラフ問題」の2つに絞って説明します。
(1)知識問題について
例えば血糖値を下げるホルモンとして有名な「インスリン」について覚えるとき、単に名前だけ覚えるのではなく、その前後にまつわる知識も一緒に覚えてしまいます。
①血糖値が上昇するとすい臓のランゲルハンス島のB細胞がこれを感知する。
②視床下部でも感知され、副交感神経を通してB細胞を刺激する。
③B細胞からインスリンが分泌される。
④肝臓や筋組織でグルコースをグリコーゲンに変えて血糖値が減少する。
⑤脂肪組織や筋組織でのグルコースの取り込み、脂肪への転換を促進することで血糖値が減少する。
このように前後関係も含めて覚えておくと、単にインスリンに関する知識だけでなく、他の大切な用語や作用も理解でき、深い知識が身につきます。また2次試験において記述問題を解く際にも、このように箇条書きで覚えておくと役に立ちます。
(2)グラフ問題について
生物はグラフが多く登場する科目です。グラフの理解が不十分な場合、読み取りが出来ず、解答を見つけることが出来ない悪循環に陥ります。グラフを制することが生物を制するといっても過言ではありません。
有名な「光の強さと光合成速度」というグラフがあります。このグラフは横軸が光の強さでわかりやすいのですが、縦軸が二酸化炭素の吸収速度になっており、縦軸の数値がそのまま光合成速度になっていないことから読み取りが難しくなっています。光の強さが0のとき、なぜマイナスからスタートするのか、呼吸による二酸化炭素の放出という逆の要素が表れていることを理解しておく必要があります。
グラフにまつわる問題はパターンが決まっています。重要な例題や類題を繰り返し演習することで、理解が深まります。知識を積み重ねた次のステップは、グラフを克服することに重点を置きましょう。
生物は知識問題とグラフ問題を解けるようになると、飛躍的に点数がアップします。問題集をどんどん解くことも大切ですが、今一度「覚えること」と「グラフの読み取り」に時間をかけるように心がけましょう。
開成ハイスクール 数学科 東山 元晴


カテゴリー: ブログ, 大学受験 | コメントは受け付けていません。
2017 年 8 月 7 日
「朝顔につるべ取られてもらい水」千代女
これはよく知られている俳句の一つで、一般には、「朝顔につるべ取られてもらひ水」という形で知られています。ところが千代女の直筆には「顔や」と書かれているものがあります。(「に」から「や」に推敲)。
では「に」と「や」ではどのような違いがあるのでしょうか。なんだか古文の問題のようで申し訳ありません。文法的にはどちらも間違っていません。それならどっちがいいのでしょうか。わかりやすいのは断然「に」の方です。朝早く起きて井戸まで水を汲みに行くと、朝顔のつるが釣瓶(の綱?)に巻きついていました。そこで擬人法的にこう詠んだと解釈できるからです。わざわざ「もらひ水」をした理由がはっきりしていますね。
それが「や」だと少々複雑になります。俳句の「や」はいわゆる「切れ字」ですから、一度そこで文が切れます。そのため朝顔と「つるべ取られて」以下が直接結びつきません。そのかわり「朝顔や」とすることで、何より朝顔の花の美しさに感動していることが感じられます。一方「朝顔に」では、朝顔の花の美しさが伝わりにくいのではないでしょうか。それぞれ一長一短があるのです。もちろんつるが巻きついているだけですから、それをほどいてあるいはちぎって、水を汲むことも可能です。そうしないで近所で水をもらうところが千代女の優しさであり、この句の見所ではないでしょうか。
朝顔は英語では、morning gloryといいます。直訳すると「朝の輝き」、なんだかカッコいいですよね。ちなみに朝顔は、アメリカやヨーロッパではそれほどメジャーな植物ではないように思います。日本人にとってみれば、昼になるとしぼんでしまうその儚さゆえに美しく感じるわけですが、欧米の人からすると、「それだけしか咲かないなんて」と思ってしまうのかもしれません。
花名の朝顔は、朝に花を咲かせ、昼にしぼんでしまう様子を「朝の美人の顔」にたとえた「朝の容花(かおばな)」の意味といわれています。朝顔の花言葉は、「はかない恋」「固い絆」「愛情」。花言葉の「はかない恋」は花が短命であることから、「固い絆」は支柱にしっかりとツルを絡ませることに由来します。
日本には奈良時代末期に遣唐使によって中国から伝わった朝顔。牽牛子(ケンゴシ)という別名は、種子に下剤や利尿剤としての効果があり、中国では牛と交換されるほど高価だったことに由来します。江戸時代に2度の朝顔ブームが起こり、それを機に品種改良も進み観賞用植物となったそうです。
今日は立秋、暦の上では秋が来たとはいえ、まだまだ暑い日の続く8月、まだ涼しい朝に早起きし、勉強の前に朝顔など眺めてはいかがですか。
開成ハイスクール 英語科 松本 雄


カテゴリー: 大学受験 | コメントは受け付けていません。
2017 年 7 月 24 日
ある村に、ヒツジ飼いの男の子がいました。来る日も来る日も、仕事はヒツジの番ばかり。男の子はあきあきしてしまい、ちょっといたずらをしたくなりました。
「たいへんだ!オオカミだ。オオカミだ」
皆さんご存知の、イソップ寓話です。何度も嘘をついて、とうとう信用されなくなってしまった少年の話ですが、どうして信用されなくなったのでしょう?「嘘をついたからじゃないか」と当然思うでしょうが、ここでは、少し数学的に考えてみることにします。
村人はおどろいて、かけつけてきました。それを見て、男の子は体を折り曲げて大笑いしていました。
最初、村人は驚いて駆けつけてきました。少年を信用していたのですね。しかし、この1回の嘘で少年の信用度は下がったはずです。どれくらいになったかを見積もることにしましょう。実は、こういったことを扱う数学として、高1で習う条件付き確率があります。そこで少し状況を整理しておきましょう。「少年は正直に言っている(H)か、嘘をいっているか(L)のどちらか」です。そして「狼は来ている(C)か、来ていないか(N)のどちらか」です。いつでも嘘を言うわけではないですし、正直に言ったつもりが、見間違いで狼が来ていると勘違いしている恐れもありますから、(H)=(C)ではないですし、(L)=(N)でもないですね。色々と入り組んでいますので、定量的に見間違いが起こる確率などを設定して状況を整理してみます。
正直に言っている(H)ときに、狼が来ている(C)=正しく警告をする確率を 70%
正直に言っている(H)ときに、狼が来ていない(N)=見間違いをする確率を 30%
としてみましょう。10回中3回の見間違いは多いのでは、と感じる人もいるかもしれませんが、まだ少年なので、それほど熟練の羊飼いではない、ということにしておきます。一方、
嘘を言っている(L)ときに、狼が来ている(C)=羊が食べられる確率を 10%
嘘を言っている(L)ときに、狼が来ていない(N)=村人が騙される確率を 90%
にしてみます。村人はかなりの高確率(90%)で騙されると思ったからこそ、少年は嘘をついたのでしょう。さて、少年は1回、嘘をついてしまいました。信用度はどれくらいになるでしょう?何を見積もればいいかは、条件付確率の公式が教えてくれます。狼が来ていない(N)という結果のもとで、少年が嘘をついた(L)のは何割くらいかを考えればいいのですから、高校の数学が教えることによれば、
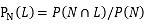
を計算すればいいことになります。今は、狼が来ていない(N)という結果が判明していますから、分母(母数)に、狼が来ていない(N)確率をもってきて、分子に、そのうち嘘をついていた(L)確率を持ってくる、というのがこの式の意味です。確率とくるとピンとこない人は、確率を総数と読み替えれば、これが「嘘つき度合い」を表すということに納得するでしょう。では、分母、分子を計算してみます。分母は、狼が来ていない(N)確率なので、①正直(H)→狼が来ていない(N)の場合と、②嘘(L)→狼が来ていない(N)の2通りを足せばよく、
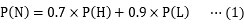
で計算できます。少年が正直者かどうかは最初のうちはわかりませんが、わざわざ嘘をつく人はそんなに大勢いないので、正直者は 8 割いるとします。
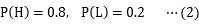
その結果、
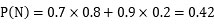
となります。次に分子ですが、それは今計算した (1) の式のうち、②嘘(L)→狼が来ていない(N)部分になるので、
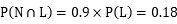
になります。したがって嘘つき度合いは、
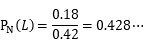
2割くらいしか嘘をつかないと思われていたのが、4割強、嘘をつくとみなされるようになりました。かなり「嘘つきだ」とみなされるようになってしまいました。しかし、まだ「嘘つき度合い」は半分以下です。少年は図に乗ってしまいました。
何日かして、男の子はまた大声をあげました。「たいへんだ!オオカミだ。オオカミだ」村人は、こんども飛び出してきました。男の子はそれを見て、またもや大笑い。村人は怒って帰っていきました。
「嘘つき度合い」はまだ半分以下だから、村人は飛び出してきたのでしょうか?何はともあれ、村人はまた騙されてしまいました。少年の信用度はどうなったでしょう?1回目の経験を考慮して(2)の式のところを
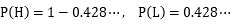
と「嘘つき度合い」が4割強になった数字で同じ計算をしてみます。その結果は、
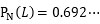
とうとう、「嘘つき度合い」が7割近くになってしまいました。この後、どうなったでしょう。皆さんご存知のとおり
ところがある日、本当にオオカミがやってきて、ヒツジの群をおそいました。男の子はあわてて、叫び声をあげました。「オオカミが来た!オオカミが来た!本当にオオカミが来たんだよ!」けれども村人は、知らんぷりです。なんども嘘をいう男の子を、だれも信じようとはしなかったのです。かわいそうに、男の子のヒツジは、オオカミにみんな食べられてしまいました。
嘘はつかないほうがいいですね。
ん、オッといけない、この文章の表題は「数学と科学・技術」でした。今の話は、どう科学に関連しているのでしょう。実は、今の思考過程を検討してみると、「狼は来なかった」という結果から、「少年は嘘つきである」という原因を探る、ということをしていたと考えることができます。このように結果や、経験をもとに、原因を探るという手法は色々な分野で応用がなされています。例えば、「この薬を飲んだら体調がよくなった」から「薬には薬効がある」という結論を定量的に出す(薬にはフラシボー効果というのがあって、薬効がなくても体調がよくなることがあるので、本当に効くかどうかを、客観的に測らないといけないのです。)などが有名ですし、「不良品が発見された」から「A工場が怪しい」という結論を出す問題は、高校数学の問題集にも載っていますね。世の中には色々な数字が飛び交っています。その中で正しく考えるというのは難しいことですので(特に確率の問題はよく誤解が起きるといわれています。)、若いうちにしっかりと学んでください。
開成ハイスクール数学科 村上豊


カテゴリー: ブログ, 大学受験 | コメントは受け付けていません。
2017 年 7 月 17 日
いよいよ夏本番。目の前には夏休みが待ち構えています。高3生にとっては正念場と言ってもいいこの夏休みをどう過ごすか、とても大事ですね。今回は短期戦、長期戦の両方の面から「計画」について考えてみたいと思います。
私は高校3年間部活動に明け暮れ、引退は高校3年の11月。もちろん夏休みは練習、練習、試合、練習と休む間もありませんでした。11月に引退したとき、来るべき1月のセンター試験、3月の2次試験までどう過ごすのかというのは大きな課題として私の上にのしかかりました。わずかな時間で成果を上げるには時間を少しも無駄にはできません。そのために「計画」がとても重要だったのです。周りのいろいろな意見を参考に自分なりに計画を立てました。ある人は大まかな長期予定を立て、それを日ごとに分割。毎朝、細かいその日のタイムスケジュールを作り、その通りに取り組んでいました。またある人は使用する教材を決定すると、教材に合わせて期日を決め解き進めていくというスタイル。その他にもいろいろな計画の立て方がありました。その中で私が採用したスタイルは「期間設定型計画法」です。私は最初に「今日から2週間数学」「その後2週間物理・化学」「その後1週間で英語」という期間を設定したプランをスケジュール帳に書き込みました。そして期間を設定した中で、具体的なスケジュールを割り振るといったプランニングです。また、一日のタイムスケジュールは「10時から夜10時までで10時間勉強」「日曜は絶対勉強しない」という、これも期間を定めるルールから始めました。そして、この通りに解き進め、受験を乗り切りました。
さて、この計画には私自身の性格に合わせた2つのポイントがあります。1つは2度勉強できない「背水の陣」を盛り込んだことです。時間に制約がある私にとって2度同じことを勉強するだけの時間はありません。だからこそ決められた期間に定めた勉強を是が非でも終わらそうという決意が生まれました。もう1つは計画を必ず成功できるように計画に「余裕」を持たせたこともポイントです。
まわりの人の例を聞いていて感じたことは「計画」は立てるだけではなく、成し遂げないといけないということです。極端な話「勉強しない」と計画で決めたなら、その時間は何があっても休憩をとるという徹底も必要です。細かい計画を積み上げることが苦手な人は、最初に中長期的な計画を立ててみることから始めると、案外細かな計画や順序が見えてくることがあります。夏は受験の天王山です。強い意志を持って、目標に向かって「計画」を成し遂げましょう。
開成ハイスクール 数学科 木村智一郎


カテゴリー: ブログ | コメントは受け付けていません。
2017 年 7 月 10 日
● 中学数学から高校数学へ
今回の指導要領変更の根幹は、知識・技能の習得・習熟からそれを活用する能力へと軸足を数歩踏み出しています。では、数学における特質は何かといえば以下の様にいえるでしょう。
①授業時間数(中1・3で+35時間)や学習内容(単元やその項目)の大幅な増加
②学習内容のレベルで発展的学習の拡張、つまり、上限撤廃への第一歩
③具体的には、指導要領中の内容区分で「数量関係」が「関数」へと表記自体を変更
では、その一端をここでご紹介しましょう。
設例1)改訂教科書での発展問題…知識の習得
関数y=ax2で、xがpからqまで増加したときの変化の割合はいくらか?
中学で学習する「関数の変化の割合」とは、x、yの増加量に対する割合なので、(中2内容)
よって、変化の割合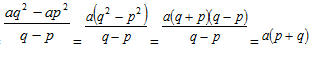 となる。
となる。
今回の改訂教科書の一部には、これを公式として取り上げるものがあります。
ところが、2011入試において、これを公式として認めず、実際の公立入試で誤り(減点)とされた答案もありました。(これは、塾では既知のものとして扱っていたためです。)
しかしながら、今後はここまでの知識習得を前提に出題されるため、正解となるでしょう。
設例2)発展問題からの授業展開…技能の習熟
図Ⅰで、放物線上の2点A、Bのx座標がp、qのとき、その直線の傾きは?
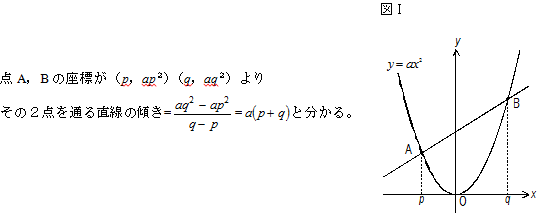
これはよく考えれば、「直線の傾き=2次関数の変化の割合」
であることを示すものです。
多少厄介な問題ですが、塾では当たり前のこととして今までも授業内にて指導しています。さらに、数学が得意なクラスでは公式として切片=-apqまでの習熟を図り、放物線上の2点のx座標から、その2点を通る直線の式:までを学習対象としています。
設例3)実際の入試問題…活用能力を試す
図Ⅱより放物線と平行な2直線の交点で、点Sのx座標の値tはいくらか?

設例4)さらに発展・昇華させると・・・
図Ⅲの放物線上の2点A、Bを通る直線の傾きは・・・(そのまま高校内容まで突き進むと・・)
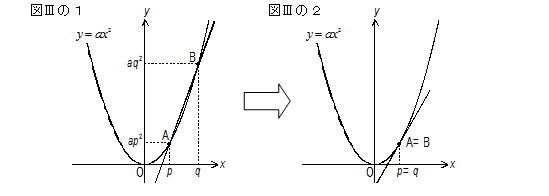
(図Ⅲの1)では、点A、Bのx座標から、その傾き=が導かれる。
ただ、ここで横軸、縦軸をそれぞれ時間軸、距離軸に擬えると、その傾きは2点間を進む「平均の速さ」を意味することとなる。さらに、ここで点Bを除々に点Aに近づけて、終に2点が重なるとき、つまり(図Ⅲの2)その直線は接線となり、その傾きは点Aにおける「瞬間の速さ」を表すことになります。すなわち、その傾き==2apとなる。
※実は、この曲線上の1点における接線の傾きが高校2年生で学習する「微分係数」と呼ばれるものです。ニュートンやライプニッツなどの巨人の肩を借りて得た微分・積分を理解することで、未知の世界(数学に限らず、広く現実世界)への扉を開き、さらなる道を探索することが可能となります。新たな世界に向けて大いなる一歩を踏み出しましょう。
※そして、これは小中高一貫教育を実施している開成教育グループだからこそ実現可能であるといえます。
最後に、若干、背伸びをしたきらいもありますが、もう一つの隠れたテーマである「理数科離れからの復権」を見通した教科書の基盤を少しでも予感していただければ幸いです。
開成ハイスクール数学科 矢倉 重人


カテゴリー: ブログ | コメントは受け付けていません。
2017 年 7 月 3 日
新しい学年の2回目の定期テストがいよいよ始まった高校も多いのではないでしょうか。中間テストで思ったほど点数が取れず、悔しい思いをした方も少なくなかったかもしれません。特に高校1年生は中学校時代とは違い科目の多さに圧倒されテストの準備が不十分だった科目もあったかもしれません。しかし、中学校のときと同様で範囲内の勉強をきちんとすれば点数が取れるテストですから、試験前の準備が大切ですね。残りの時間でしっかり準備をしましょう。
定期テストが終わると夏休み。1学期の積み残しがある方、特に英数に課題を多く抱えている方は夏期講習会を利用しましょう。復習はもちろんのこと、2学期の準備もいち早くできるのでこれからの高校生活も安心です。詳しくは各教室にお問い合わせください。
さて、その夏休みですが3年生にとっては受験生として実力をつける絶好の機会です。塾の自習室にこもって朝から晩まで勉強しようと既に計画を立てている方も多いと思います。
大正解です。この夏の充実度合が2学期からのあらゆる模試で結果として出てきます。楽しみですね。量、質ともに確保してこの夏を乗り切ってください。
では1年生、2年生はどうかといえば…こちらのお話は何度も、いろいろな先生から、先輩から聞いている話だとは思いますが、もう一度ここで言わせてもらいます。大学受験のほとんどが「高1、高2の内容」です。今の高1生が最後のセンター試験受験者となるわけですが(ちなみに私は最初のセンター試験を受けました…)センター試験の数学は「数Ⅰ・Ⅱ」「数A・B」です。すべて高校2年生まで、実際は高2の秋までで終了する内容です。となれば今習っている内容が大学入試でも必要になるわけですから、今のうちに片づけておくことが必要なのは、もうみなさんもわかっていることと思います。クラブも忙しい、思い出作りも忙しいけれども大学受験の土台作りにも時間をかけましょう。そうすれば第1志望校への道を周りのライバルより先に進むことができると思います。
と偉そうにお話をしてきましたが、かく言う私は思うような結果にはなりませんでした。高2まで夏休みをクラブで過ごしてしまったからです。高3の夏だけでは間に合いませんでした。
みなさんの夏はこれからです。今年は特に暑いとの予報です。涼しい自習室で快適に夏を過ごしませんか。
開成ハイスクール 数学科 秋田純一


カテゴリー: ブログ | コメントは受け付けていません。




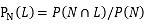
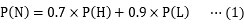
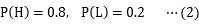
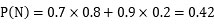
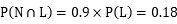
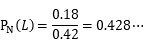
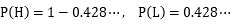
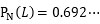
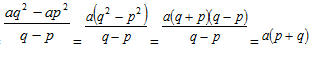 となる。
となる。