2次関数から微分・積分へ
2017 年 7 月 10 日 月曜日● 中学数学から高校数学へ
今回の指導要領変更の根幹は、知識・技能の習得・習熟からそれを活用する能力へと軸足を数歩踏み出しています。では、数学における特質は何かといえば以下の様にいえるでしょう。
①授業時間数(中1・3で+35時間)や学習内容(単元やその項目)の大幅な増加
②学習内容のレベルで発展的学習の拡張、つまり、上限撤廃への第一歩
③具体的には、指導要領中の内容区分で「数量関係」が「関数」へと表記自体を変更
では、その一端をここでご紹介しましょう。
設例1)改訂教科書での発展問題…知識の習得
関数y=ax2で、xがpからqまで増加したときの変化の割合はいくらか?
中学で学習する「関数の変化の割合」とは、x、yの増加量に対する割合なので、(中2内容)
よって、変化の割合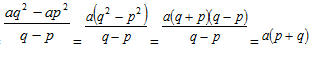 となる。
となる。
今回の改訂教科書の一部には、これを公式として取り上げるものがあります。
ところが、2011入試において、これを公式として認めず、実際の公立入試で誤り(減点)とされた答案もありました。(これは、塾では既知のものとして扱っていたためです。)
しかしながら、今後はここまでの知識習得を前提に出題されるため、正解となるでしょう。
設例2)発展問題からの授業展開…技能の習熟
図Ⅰで、放物線上の2点A、Bのx座標がp、qのとき、その直線の傾きは?
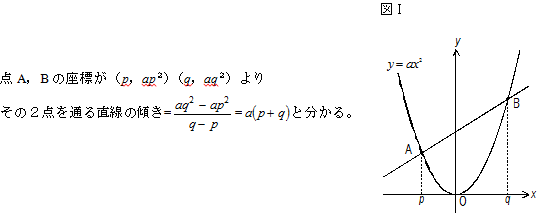
これはよく考えれば、「直線の傾き=2次関数の変化の割合」
であることを示すものです。
多少厄介な問題ですが、塾では当たり前のこととして今までも授業内にて指導しています。さらに、数学が得意なクラスでは公式として切片=-apqまでの習熟を図り、放物線上の2点のx座標から、その2点を通る直線の式:までを学習対象としています。
設例3)実際の入試問題…活用能力を試す
図Ⅱより放物線と平行な2直線の交点で、点Sのx座標の値tはいくらか?

設例4)さらに発展・昇華させると・・・
図Ⅲの放物線上の2点A、Bを通る直線の傾きは・・・(そのまま高校内容まで突き進むと・・)
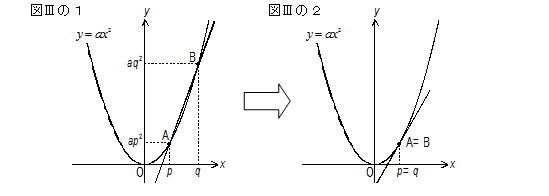
(図Ⅲの1)では、点A、Bのx座標から、その傾き=が導かれる。
ただ、ここで横軸、縦軸をそれぞれ時間軸、距離軸に擬えると、その傾きは2点間を進む「平均の速さ」を意味することとなる。さらに、ここで点Bを除々に点Aに近づけて、終に2点が重なるとき、つまり(図Ⅲの2)その直線は接線となり、その傾きは点Aにおける「瞬間の速さ」を表すことになります。すなわち、その傾き==2apとなる。
※実は、この曲線上の1点における接線の傾きが高校2年生で学習する「微分係数」と呼ばれるものです。ニュートンやライプニッツなどの巨人の肩を借りて得た微分・積分を理解することで、未知の世界(数学に限らず、広く現実世界)への扉を開き、さらなる道を探索することが可能となります。新たな世界に向けて大いなる一歩を踏み出しましょう。
※そして、これは小中高一貫教育を実施している開成教育グループだからこそ実現可能であるといえます。
最後に、若干、背伸びをしたきらいもありますが、もう一つの隠れたテーマである「理数科離れからの復権」を見通した教科書の基盤を少しでも予感していただければ幸いです。
開成ハイスクール数学科 矢倉 重人



