新指導要領と数学(その2)
2012 年 11 月 26 日 月曜日今回は、前回(6月25日掲載分)に引き続き、新指導要領の話をしましょう。前回は、情報化社会の中で使われる「統計」の話をしましたが、今回はもう一つの大きな変化である、「整数」を取り上げます。
みなさん、「整数」というものが何なのか覚えていますか?「整数」とは、1、2、3、4、・・・というように数える「自然数」と、0と、負の数(-1、-2、-3、-4、・・・)を合わせたもののことでした。ではなぜ、そんなものを習うのでしょう?ここでは、まず、「誕生日当てクイズ」ということで話を進めていくことにします。
ここに、8月22日が誕生日のS君と、その先生のT先生がいたとして、次のような会話が始まったとします。
T「さてさて、S君。私は君のことなら何でもわかっている。その証拠に、今から君の誕生日を当ててみようではないか?」
S「(なんか胡散臭い先生だな。)ええ、いいですよ。どうぞ。」
T「それでは、君の生まれた日を頭に浮かべるがよい。」
S「(22日生まれだから、22だな。)はい、どうぞ。」
T「では、その数字を10倍して、生まれた月を足してみるがよい。」
S「(えーっと、22×10に8月生まれの 8 を足して228か。)先生、変な口調ですね。」
T「わはははは、君の誕生日が見えてきたぞ。では次にその数を3倍するがよい。」
S「(暗算苦手だな、228×3で、えーっと、さんぱにじゅうしの・・・684かな)はい、出来ました。」
T「では、その数から生まれた月の2倍を引いて答えを言ってくれたまえ。」
S「はいはい。(684から2×8の16を引いて・・・、)えーっと、668です。」
T「君の誕生日を当てて見せよう。8月22日、これに相違ないな。」
S「えー、なんでわかったんですか?」
さて、以上の誕生日当てクイズの仕組みは、実は高校で習う「不定方程式」と絡んでいます。謎解きをするなら、次のようになります。(少し数式が出てきますが、我慢して下さい。)誕生日を x 月 y 日とすると、S君がした計算は次のようになります。確認してみて下さい。
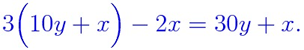
そしてS君が出した答えが668なので、
![]()
が解ければよいことになります。そして実は、この方程式(この種の整数解を求める方程式を不定方程式と呼びます)の解き方をいろいろと高校で習うことになるのです。ここでは、やり方のみを書いておきましょう。668を y の係数 30 で割った余り 8 が x の値です。すなわち、8月生まれだと分かります。一方、30で割った商 22 が y の値です。つまり 22 日生まれだと分かるのです(実際に他の誕生日でいろいろ試してみると理解が深まります)。
長々と書きましたが、どうでしょうか?単なる余興じゃないか、と思う人もいるかもしれません。ところが実は、これも、近年の情報化社会と大きく結び付いています。情報化社会では、情報を公開するだけでなく、秘密を保つ必要もあります。そして、上の話は、情報を秘密に保つという視点からいうと、次のようにまとめる事ができます。もともと8月22日という意味のあるデータが、ある計算の結果668という、意味のないデータに変わっています。したがって、単にこのデータを見ただけでは、からくりの分かっていないS君にとっては、何の数字かわかりません。ところが、暗号の作り方と解き方を知っている者(T先生)にとっては、8月22日という意味のあるデータを復元できるのです(実際の秘密通信では、暗号の作り方が分かっても簡単には解読できないような整数を使ったからくりが使われています)。
数学というものは、現代の社会の中でこっそりと応用されています。なかなか気づきにくい知恵であったりします。意味がわからないことが多くて、苦労することもあると思いますが(実際、私もそうでした)、学ぶことには果敢にチャレンジしてください。知らないで生きるよりも、知って生きる方が何倍も豊かな生き方ができますから。
開成ハイスクール数学科 村上 豊



