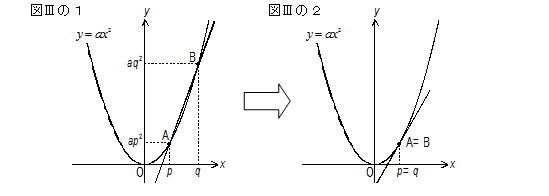
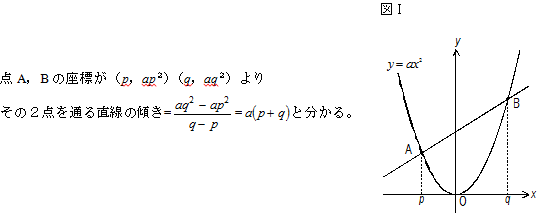数学と科学・技術 その15
2017 年 7 月 24 日 月曜日ある村に、ヒツジ飼いの男の子がいました。来る日も来る日も、仕事はヒツジの番ばかり。男の子はあきあきしてしまい、ちょっといたずらをしたくなりました。
「たいへんだ!オオカミだ。オオカミだ」
皆さんご存知の、イソップ寓話です。何度も嘘をついて、とうとう信用されなくなってしまった少年の話ですが、どうして信用されなくなったのでしょう?「嘘をついたからじゃないか」と当然思うでしょうが、ここでは、少し数学的に考えてみることにします。
村人はおどろいて、かけつけてきました。それを見て、男の子は体を折り曲げて大笑いしていました。
最初、村人は驚いて駆けつけてきました。少年を信用していたのですね。しかし、この1回の嘘で少年の信用度は下がったはずです。どれくらいになったかを見積もることにしましょう。実は、こういったことを扱う数学として、高1で習う条件付き確率があります。そこで少し状況を整理しておきましょう。「少年は正直に言っている(H)か、嘘をいっているか(L)のどちらか」です。そして「狼は来ている(C)か、来ていないか(N)のどちらか」です。いつでも嘘を言うわけではないですし、正直に言ったつもりが、見間違いで狼が来ていると勘違いしている恐れもありますから、(H)=(C)ではないですし、(L)=(N)でもないですね。色々と入り組んでいますので、定量的に見間違いが起こる確率などを設定して状況を整理してみます。
正直に言っている(H)ときに、狼が来ている(C)=正しく警告をする確率を 70%
正直に言っている(H)ときに、狼が来ていない(N)=見間違いをする確率を 30%
としてみましょう。10回中3回の見間違いは多いのでは、と感じる人もいるかもしれませんが、まだ少年なので、それほど熟練の羊飼いではない、ということにしておきます。一方、
嘘を言っている(L)ときに、狼が来ている(C)=羊が食べられる確率を 10%
嘘を言っている(L)ときに、狼が来ていない(N)=村人が騙される確率を 90%
にしてみます。村人はかなりの高確率(90%)で騙されると思ったからこそ、少年は嘘をついたのでしょう。さて、少年は1回、嘘をついてしまいました。信用度はどれくらいになるでしょう?何を見積もればいいかは、条件付確率の公式が教えてくれます。狼が来ていない(N)という結果のもとで、少年が嘘をついた(L)のは何割くらいかを考えればいいのですから、高校の数学が教えることによれば、
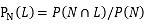
を計算すればいいことになります。今は、狼が来ていない(N)という結果が判明していますから、分母(母数)に、狼が来ていない(N)確率をもってきて、分子に、そのうち嘘をついていた(L)確率を持ってくる、というのがこの式の意味です。確率とくるとピンとこない人は、確率を総数と読み替えれば、これが「嘘つき度合い」を表すということに納得するでしょう。では、分母、分子を計算してみます。分母は、狼が来ていない(N)確率なので、①正直(H)→狼が来ていない(N)の場合と、②嘘(L)→狼が来ていない(N)の2通りを足せばよく、
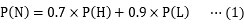
で計算できます。少年が正直者かどうかは最初のうちはわかりませんが、わざわざ嘘をつく人はそんなに大勢いないので、正直者は 8 割いるとします。
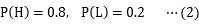
その結果、
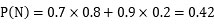
となります。次に分子ですが、それは今計算した (1) の式のうち、②嘘(L)→狼が来ていない(N)部分になるので、
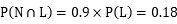
になります。したがって嘘つき度合いは、
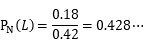
2割くらいしか嘘をつかないと思われていたのが、4割強、嘘をつくとみなされるようになりました。かなり「嘘つきだ」とみなされるようになってしまいました。しかし、まだ「嘘つき度合い」は半分以下です。少年は図に乗ってしまいました。
何日かして、男の子はまた大声をあげました。「たいへんだ!オオカミだ。オオカミだ」村人は、こんども飛び出してきました。男の子はそれを見て、またもや大笑い。村人は怒って帰っていきました。
「嘘つき度合い」はまだ半分以下だから、村人は飛び出してきたのでしょうか?何はともあれ、村人はまた騙されてしまいました。少年の信用度はどうなったでしょう?1回目の経験を考慮して(2)の式のところを
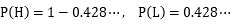
と「嘘つき度合い」が4割強になった数字で同じ計算をしてみます。その結果は、
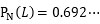
とうとう、「嘘つき度合い」が7割近くになってしまいました。この後、どうなったでしょう。皆さんご存知のとおり
ところがある日、本当にオオカミがやってきて、ヒツジの群をおそいました。男の子はあわてて、叫び声をあげました。「オオカミが来た!オオカミが来た!本当にオオカミが来たんだよ!」けれども村人は、知らんぷりです。なんども嘘をいう男の子を、だれも信じようとはしなかったのです。かわいそうに、男の子のヒツジは、オオカミにみんな食べられてしまいました。
嘘はつかないほうがいいですね。
ん、オッといけない、この文章の表題は「数学と科学・技術」でした。今の話は、どう科学に関連しているのでしょう。実は、今の思考過程を検討してみると、「狼は来なかった」という結果から、「少年は嘘つきである」という原因を探る、ということをしていたと考えることができます。このように結果や、経験をもとに、原因を探るという手法は色々な分野で応用がなされています。例えば、「この薬を飲んだら体調がよくなった」から「薬には薬効がある」という結論を定量的に出す(薬にはフラシボー効果というのがあって、薬効がなくても体調がよくなることがあるので、本当に効くかどうかを、客観的に測らないといけないのです。)などが有名ですし、「不良品が発見された」から「A工場が怪しい」という結論を出す問題は、高校数学の問題集にも載っていますね。世の中には色々な数字が飛び交っています。その中で正しく考えるというのは難しいことですので(特に確率の問題はよく誤解が起きるといわれています。)、若いうちにしっかりと学んでください。
開成ハイスクール数学科 村上豊




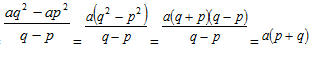 となる。
となる。