みなさん、こんにちは。高1生のみなさんは、高校生になって1ヶ月ほど過ぎましたね。高3生のみなさんは、受験学年になって、早くも1ヶ月が過ぎました。ゴールデンウィークでたるんでしまった、なんてことはないでしょうね。
ところで、高1生と高3生では学習指導要領が違っているということは、知っていますか。昨年から私はブログで、指導要領が変わった点のうち、いくつか数学こぼれ話のようなことを書いてきましたが、今回も同様に、ちょっとしたことを書いていくことにします。 今回とりあげるテーマは「複素数平面」です。「複素数平面」は新しい指導要領では、(主に理系が高3時に選択する)数学Ⅲの分野に含まれています。「では、私は文系だから読まなくていいや」と思う人もいるかもしれませんが、少しだけ話に付き合って下さい。
さて、「複素数平面」の話しを続けていきますが、その前に皆さんは中学生のときに、(マイナス)×(マイナス)は(プラス)だと習ったと思います。ところで、それが、何故だか考えたことがある人はいるでしょうか?そんなもんだ、と思った人もいれば、よく分からないままに覚えてしまった人もいるでしょう。ここでは、少し図形的に説明してみることにします。まず、
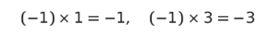
は、皆さん納得しているものとします。そこで、この式を数直線を使って理解してみましょう。
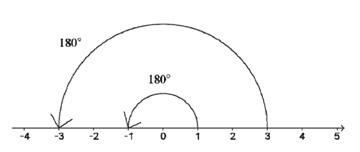
すると、上の図のように、(マイナス)をかけることは、数直線上で言えば、180度反対側に行くことになります。ということは、どういうことでしょう。もう一回(マイナス)をかければ、もう一度180度反対側に行くことになると考えるのが妥当ではないでしょうか?
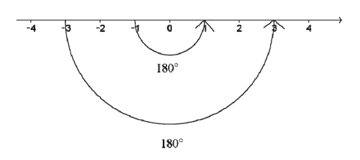
したがって、そのことを図で表すと上の図のようになります。ここで、全体を振り返ってみましょう。最初に(マイナス)をかけることで180度回転しました。次に、もう1回(マイナス)をかけることで、さらに180度回転しました。したがって、全体で合計360度回転して元の(プラス)に戻ることになるのです。
さて、以上で(マイナス)かける(マイナス)が(プラス)であることの説明を終えますが、実はこのことと「複素数平面」の話がつながっています。主に高校2年で習う数Ⅱの範囲に、2回かけると(マイナス)になる数(これは、 と書くことになっています。虚数単位という難しい名前がついています。)を習います。そんな数があるはずがないと思う人が大半ですが、上で説明した「(マイナス)をかけることは、180度回転することに等しい」ということを考えると、
「 という数を2回かけると(マイナス)になる。」
→「 という数を2回かけると180度回転する。」
→「 は1回かけると90度回転するはず!?」
という発想をもつことができます。
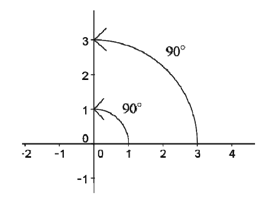
こうして、もともと数直線上だと考えていた数を、平面全体まで広げて考えてみようか、ということで「複素数平面」が生まれてきました。人間の発想って不思議で柔軟ですね。しかし、みなさんの中には、「そんなのは、頭の中で考えているだけで、実際には なんて数はないでしょ。」と思う人もいるでしょう。ところが、この という数が「原子や分子の世界」を理解するのに使われたり、「電気製品の設計」をするのに使われたりするようになったのです。このあたりは高校の数学だけを見ていてもさっぱりわからない世界ですが、ときには、こんな話を聞いてみるのもいいのではないでしょうか。自分一人で知っている範囲のことはそんなに多くはありません。むしろほとんどないと言ってもいいくらいです。勉強し、いろいろな人の話を聞き、自分の中に良いものを蓄えていくようにしてください。
開成ハイスクール数学科 村上 豊






