数学と科学・技術 その7
2015 年 10 月 26 日 月曜日みなさん、こんにちは。すっかり秋になりました。秋といえば、「食欲の秋」「スポーツの秋」「読書の秋」「芸術の秋」など様々な秋がありますが、みなさんはどんな秋を過ごしているでしょう。
さて、前回は2次関数(と平均)の話をしましたが、今回は3次関数について話すことにしましょう。微分を習った人は3次関数のグラフが次のような形になる、ということを計算で求めたと思います。
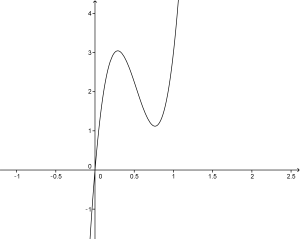
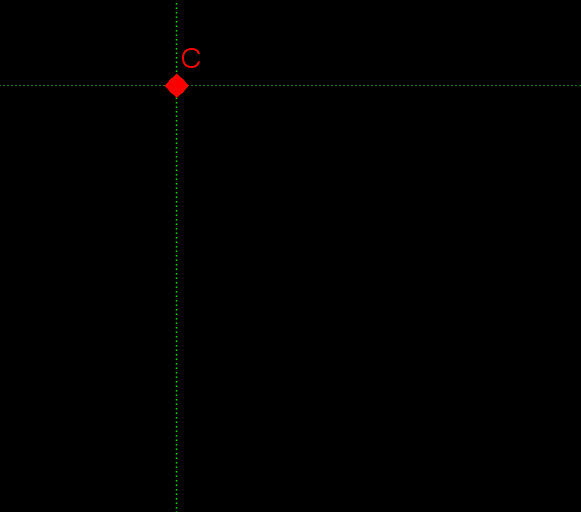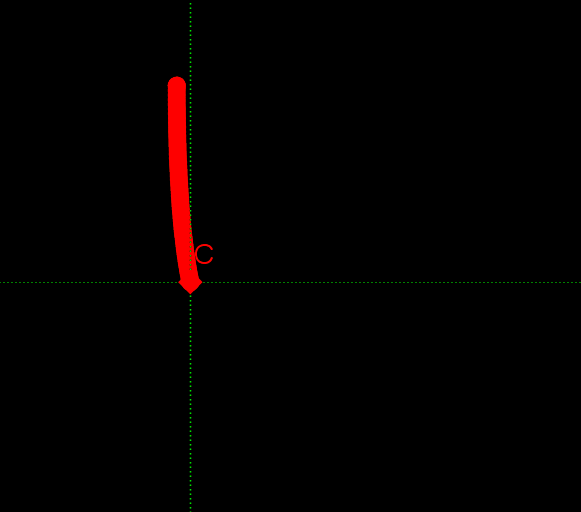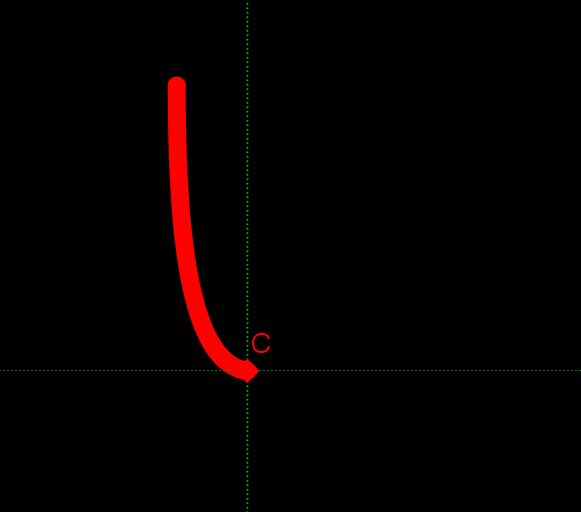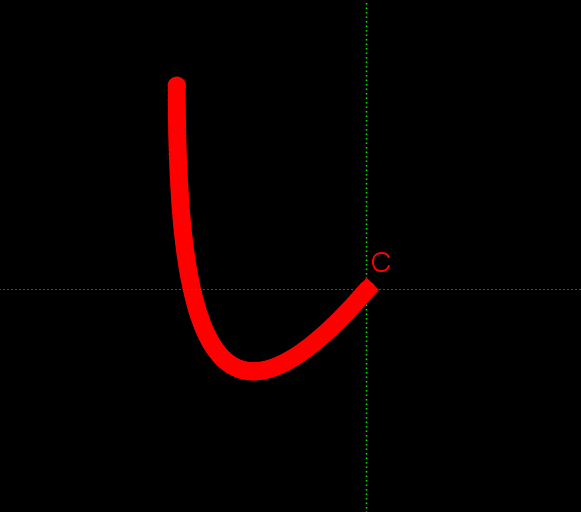
なにか、グニャグニャした形ですが、微分の計算をして、増減表を書いて、極大値や極小値を求めて…、とにかくいっぱい計算して、結局なんだったんだ、と思った人もいるでしょう。ここでは、この3次関数の応用を話すことにします。そのために、上のグラフの解釈を変えて、横軸を時間、縦軸を水平方向の位置だと思うことにします。すると、グラフは、次の水平方向に動く点となります。
グラフが上下に変化しているのに合わせて、点が左右に動いていることが分かります。ちなみにこの3次関数は
![]()
で表される関数です。他に、
![]()
を使ってみると、

こんな動きになります。今回は左右ではなく、上下に動かしてみました。
「別段変わった動きでもない、つまらない」と思うでしょうか?私もそう思いますが、では、この二つの動きを合成してみたらどうなるでしょう。左右の動きと上下の動きを同時に行ってみるのです。すると、次のようになります。
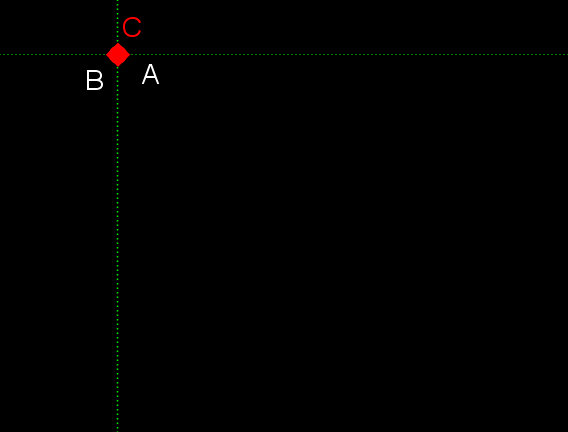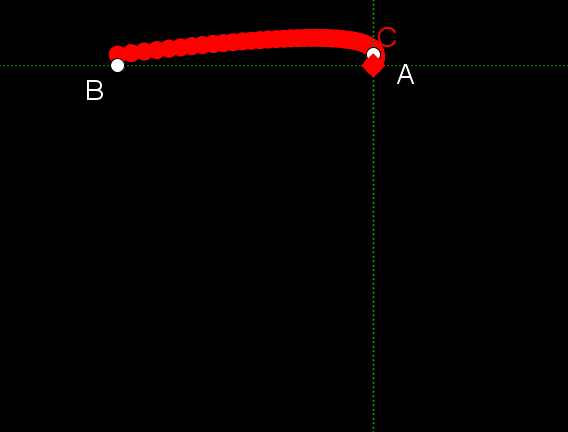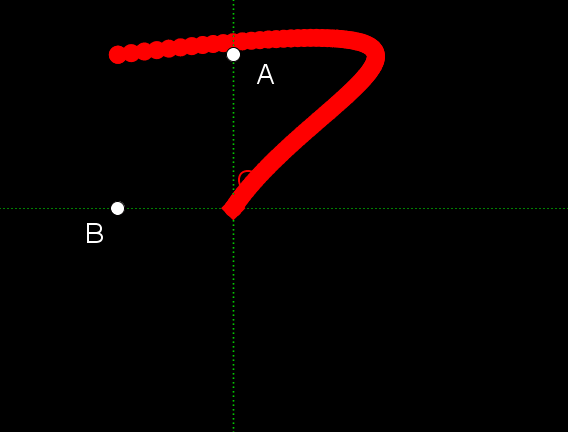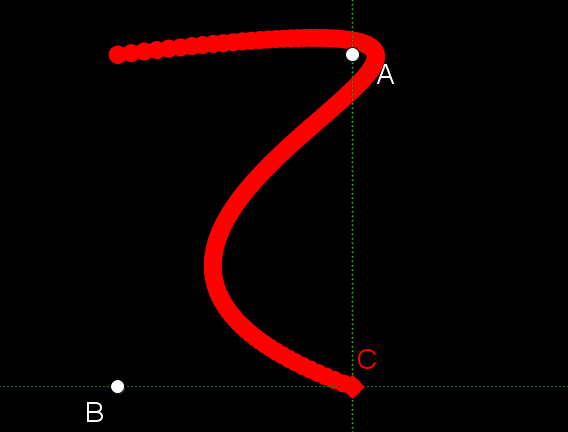
![]()
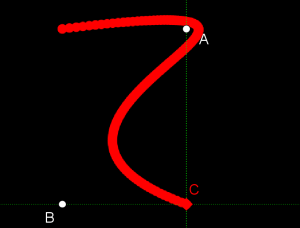
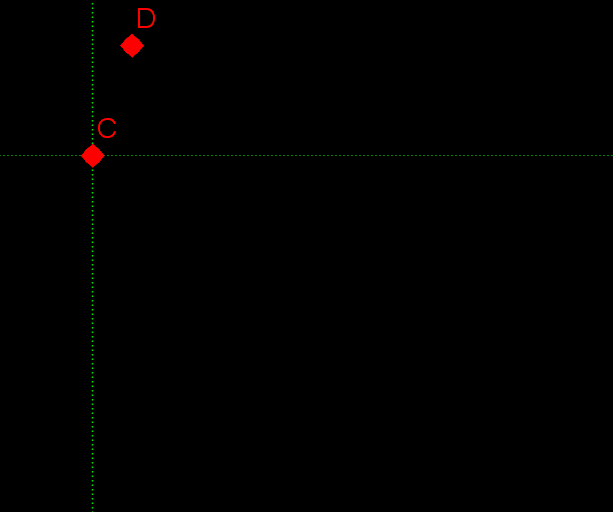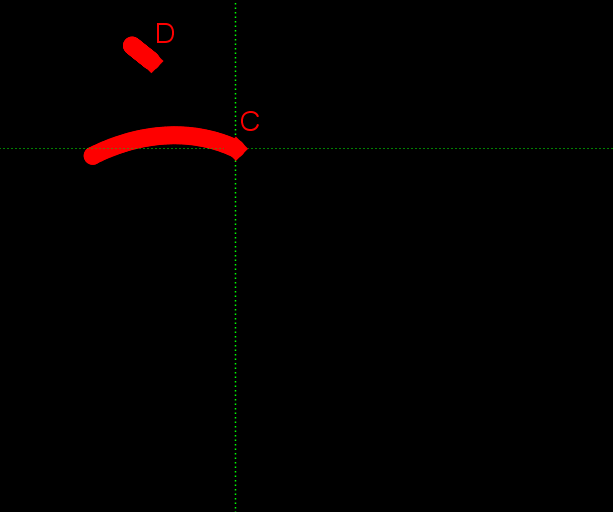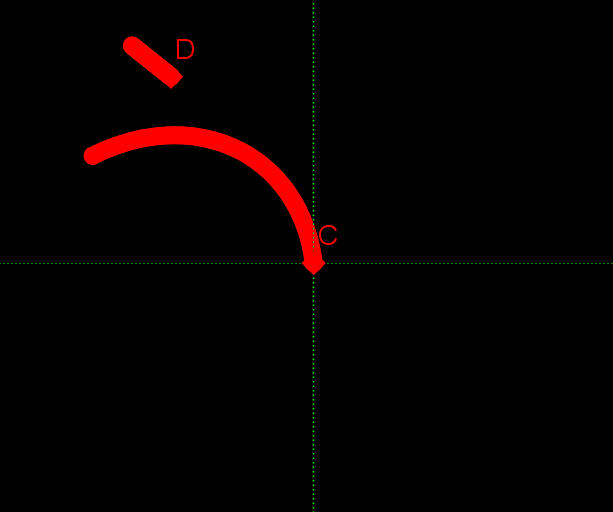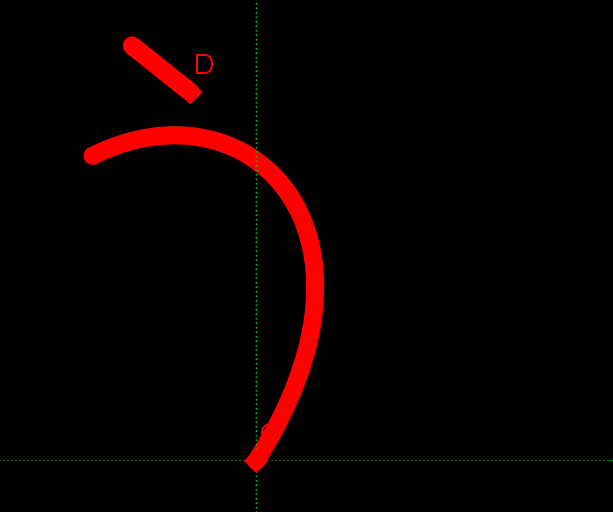
アニメーションが早く切り替わるので、右側に完成品を載せています。「て」という字が書けていることがわかるでしょう。そういわれて振り返ってみると、元々の左右の動きや、上下の動きは、「て」という字を書くときの手の動きのような気がしてきませんか?
現在は、生活のさまざまなところにコンピュータが入り込んでいますが、そこで見ることのできる、文字やCG、イラストなどは、実は3次関数(3次のベジェ曲線)を使って描かれることがよくあります。もちろん実際は、3次関数を複数使うことで、上の下手くそな「て」ではなく、きれいな文字の「て」を描いていたり、数式をそのまま使うのではなく、直感的に描けるような工夫がなされていたりします。その基礎的な部分には数学が使われているのです。「数学は科学の女王である」と言われることがあります。「科学・技術」について、ほとんど意識せずとも日々の生活は送れますが、現代の私たちの生活を支えているのも事実です。できる限り慣れ親しみ、生活を実りあるものにしてください。
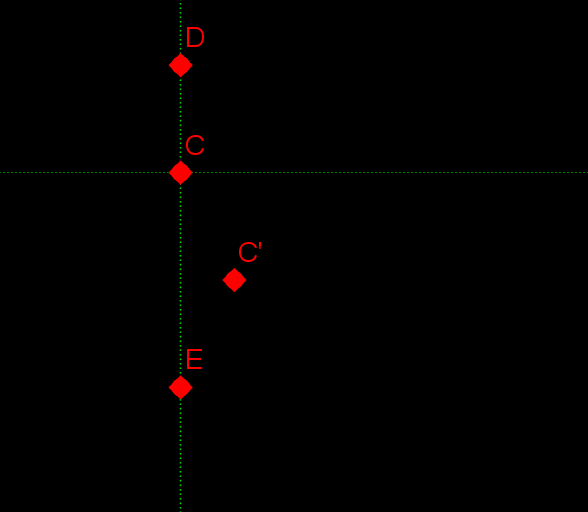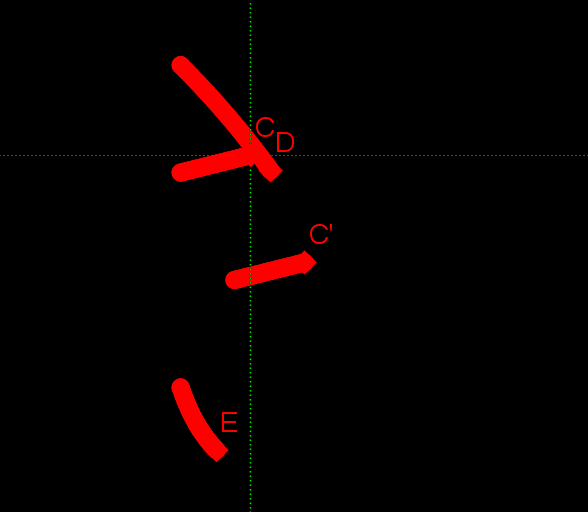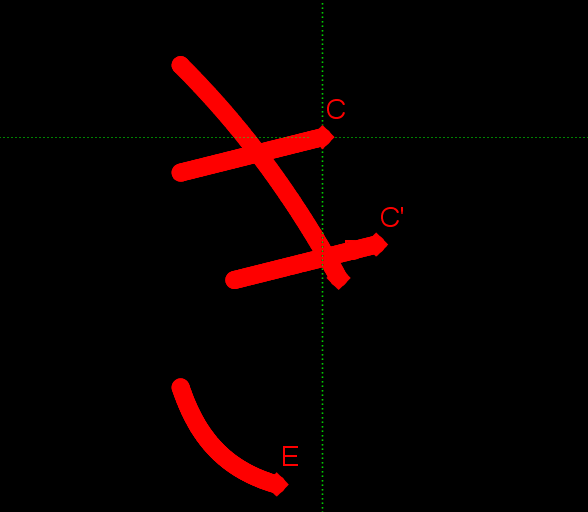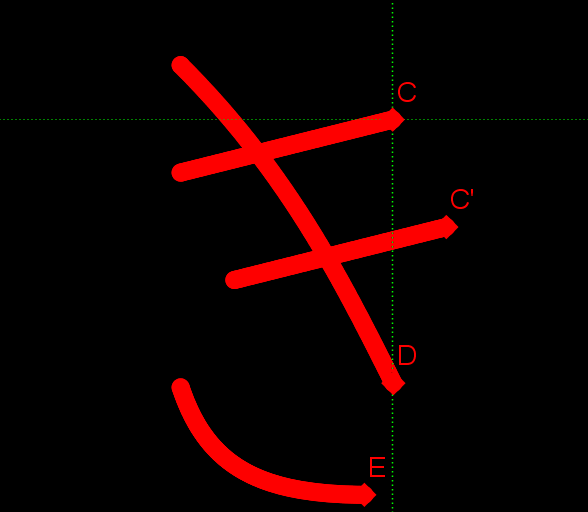
最後におまけとして、数式で描いた「すうしき」(下手ですが)と、「す」のくるっと回る部分の数式を載せておきたいと思います。
開成ハイスクール数学科 村上豊
![]()



