数学と科学・技術 その19
2018 年 6 月 1 日 金曜日皆さん、こんにちは。今回は「面積・体積」ということを切り口に話を進めたいと思います。皆さんは、面積の公式というと、三角形の面積公式、「(底辺)×(高さ)÷2」を思い出すでしょうか?それとも円の面積公式「(半径)×(半径)×(円周率)」を思い出すでしょうか?ひょっとしたら、高校で三角比を習ったときに出てきた
![]()
を思い出す人もいるかもしれませんし、ヘロンの公式などが出てくる人もいるかもしれません。高校の数学になると面積の公式も様々な形で出てきます。また、数Ⅱになれば、三角形だけではなく、放物線と直線によって囲まれた図形の面積、
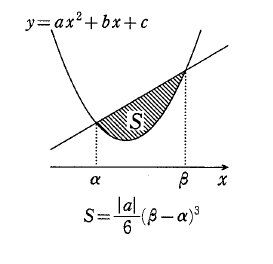
それを「6分の1公式」として知られている積分を使って計算できるようになりますね。このように、高校になると、数学を使って扱える範囲が広がってくるのですが、ところで皆さん、小学校のときに次のような問題「下の図のような池の(およその)面積を求めよ」を扱ったことがあるのを覚えているでしょうか?
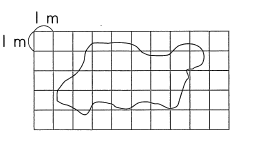
実際の池などは、三角形や、放物線のような簡単に数式で表すことができないため、面積の公式などを作ることができません。では面積は一体どうすれば測れることになるのでしょう?実は、上の小学生のときの問題にヒントが隠されています。図には1メートル四方の正方形が書かれていますが、もしそれが1センチメートル四方の正方形にしてマス目の個数を数えたらどうなるでしょう?1メートル四方のときよりも、より本当の池の面積に近づくと思いませんか?さらに1センチメートル四方を1ミリメートル四方にしたら、もっと小さく1マイクロメートル四方にしたら、さらに小さく原子1個分の大きさにしてしまったら、・・・。このように考えていくと細かく分けていくことで、より正確に面積を計算できるということが想像できると思います(実際に実行するのは手間がかかりますが)。そして実はこの考え方こそが、高校で習う「積分」の起源になっています(数Ⅲを履修すれば、「区分求積法」のところでその考え方を学びます)。より細かく分けて、それらを積み上げること、そうすることで、古代ギリシャの時代には
など、小学生のときに習った公式の不思議な数、3分の1や、3分の4が導かれています。当時は、微分も積分もなく、数式すらなかった時代ですが、その考え方の道理は今現在でも「なるほど」と思えるものだと思います。単なる公式だけの暗記で終わらないよう心掛けてください。
ところで、この細かく分けて、それらを積み上げる=積分という考え方は実用でも使われています。上の説明では、長さを細かくわけて計算する、という考え方を説明しましたが、では時間を細かく分けて計算する、と発想を変えてみたらどうなるでしょう。例えば、電気料金は1か月ごとに使用した電気量に従って請求されますが、その電気量はどうすれば正確に測れるのでしょう?上の説明と同じように、1日単位で測る⇒1時間単位で測る⇒1分単位で測る⇒1秒単位で測る⇒・・・、とどんどん細かく図る単位を変えていけばいいのです。家庭で使用する電気量は、電気メータで測られていますが、何か円盤のようなものが回っているのを見たことがある人もいると思います。ほんの少しの時間で、使った電気量に応じて円盤が少しまわる、そういったことを連綿と繰り返すことでメーターの数字が少しずつ増えていって、最終的に1か月の使用料を計算しています。このように細かく分けて考えることで、様々なものが正確に理解できてしまうのです。身近なものにもこういった仕組みはいろいろなところで使われています。少し回りを探してみて考えてみるのもいいかもしれませんね。
開成ハイスクール数学科 村上 豊



